アルゴリズムのとびら　その2

はじめに

プログラミングにおいて、アルゴリズムはとても大切な役割を果たします。
アルゴリズムは、私たちが直面する問題を効率よく解決するための手順であり、プログラムがどのように動くかを決める重要な要素です。

「アルゴリズムのとびら」シリーズの2回目は、前回に引き続き、重さの上限が決まっている中で合計の値段が一番高くなる組み合わせを探します。
お宝の数が増えると組み合わせの数もどんどん増えますが、ベストな組み合わせを効率よく探す方法はあるでしょうか？

勇者ねこの冒険

前回見つけたお宝のおかげで船を手に入れた勇者ねこ。
海を冒険して、小さな宝島を発見しました！

「今度はお宝が5つあるぞ」

お宝	重さ	値段
Aのお宝	5kg	400ポイント
Bのお宝	8kg	600ポイント
Cのお宝	15kg	1800ポイント
Dのお宝	12kg	1500ポイント
Eのお宝	10kg	1000ポイント

「今の船だと、20キログラム以内ならのせられるぞ」

「ええっと、2つ持って帰る組み合わせが10通りあって……」
「全部の組み合わせを考えるだけでも大変だ！」

「もれやかぶりがないように、図に書いてみよう」
「順序が違うだけの組み合わせは書かなくていいから、Aのお宝からかいていくとこうなるかな」

「一番上の段はお宝を持って帰らない場合で、次の段は1つだけ持って帰るパターン、その次の段は2つだけ持って帰るパターン…というふうになるね」

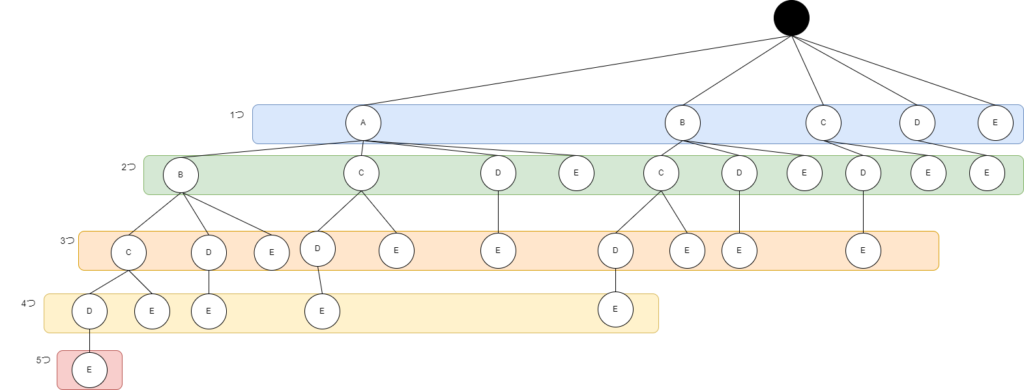
「効率よく計算する方法はないかな？」
「とりあえず図の上から順に重さと値段を計算していって…」
「あ！　図の途中で重さが20キログラムを超える結果が出た！」

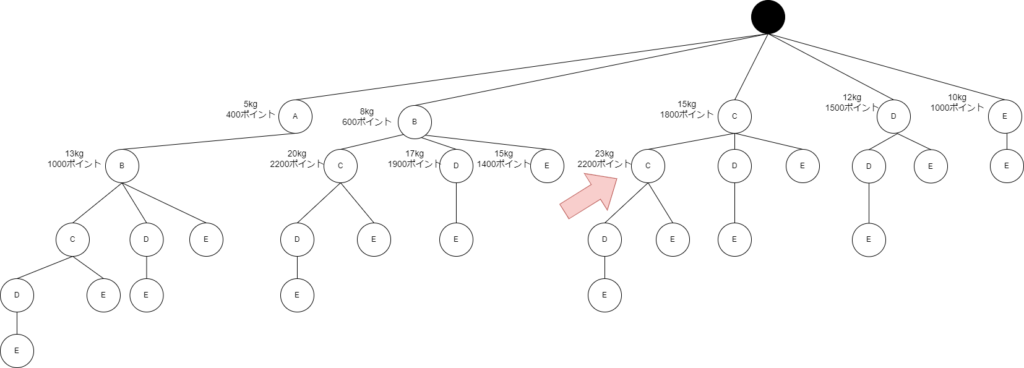
「じゃあ、ここからつながっている下の部分も20キログラムを超えるはずだから、そこはもう計算しなくていいや」

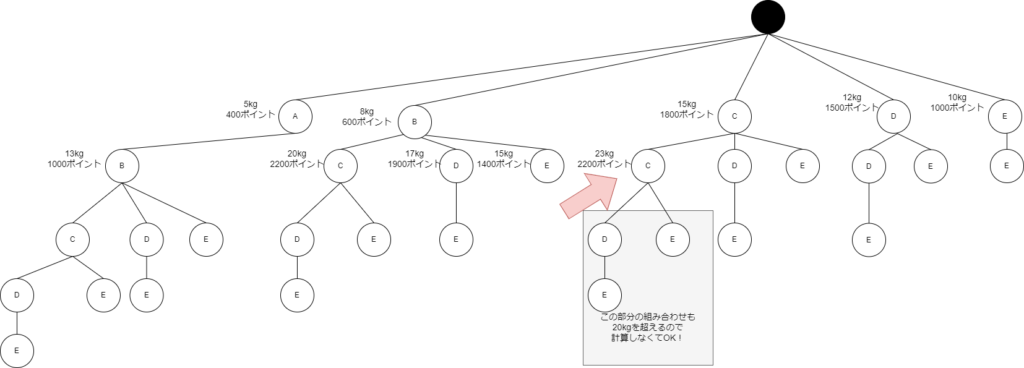
「図にしたおかげで計算する部分を少し減らせたぞ」
「結果がこうなったから…」

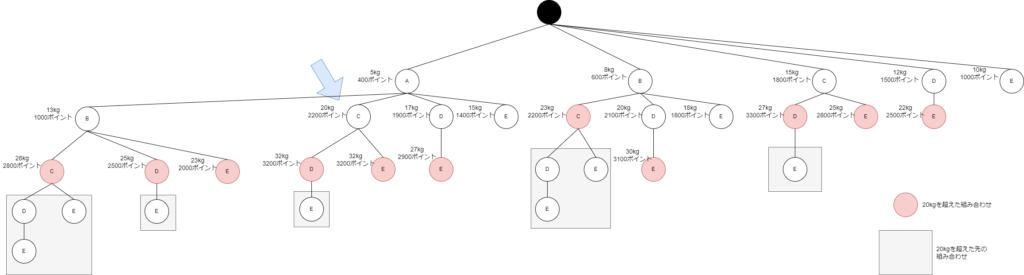
「20キログラム以内で一番値段が高い組み合わせは、こうだ！」

Aのお宝とCのお宝　20kg 2200ポイント

勇者ねこは無事にお宝を持ち帰りました。やったね！

解説

今回の冒険では、お宝の数が前回よりも多く、全ての組み合わせを考えるのが大変になりましたね。
組み合わせが増えると、その分計算する量も増えてしまいます。
今回のようにお宝が5つあると、持って帰る組み合わせは2の5乗（32通り）になります。
お宝それぞれに「選ぶ・選ばない」の2通りがあるので、お宝の数をNとすると組み合わせは2のN乗と表せます。
このように、お宝の数が増えると組み合わせの数は指数的に増加するため、すべてを計算するのは時間がかかります。

そこで、勇者ねこがやったように、効率よく計算する方法が重要になります。
今回使ったのは、枝刈り（えだかり）と呼ばれる手法です。枝刈りとは、途中で条件に合わないと分かった組み合わせを計算から省くことで、無駄な計算を減らす方法です。

図を使って順番に重さと値段を計算し、重さの制限（20キログラム）を超えた場合、その先の組み合わせを計算しないようにしたため、時間を節約できました。

次回は、さらに効率の良いアルゴリズムを使って、もっと多くのお宝の中から最適な組み合わせを見つける方法を紹介します。お楽しみに！